We use the term tree to mean a rooted, ordered, labeled
tree, such as those depicted in Figure 1. (Computer
scientists like to draw their trees upside-down.) Each tree has a
unique ``top'' node called its root. In the figure, the node
numbered 1 is the root of tree 
. (The node number is used to
identify a node and is indicated within the circle representing the
node.) Each node in a tree also has a label, which is indicated
next to that node in the figure. For this problem, we assume that
labels are real numbers. For example, the label of node 4 is 4.40.
Each node except the root also has a unique parent node. In
the figure, we connect a node to its parent (depicted above the node)
using a line. For example, the parent of node 7 is node 1. A node is
called it's parent's child. Nodes that do not have any children
are called leaf nodes; the rest are called interior
nodes. The children of each interior node are ordered, and the
figure depicts the children of each node left-to-right in this order.
For example, the children of node 2, in order, are 3, 4, and 6.
All the nodes that lie on the path (of length zero or more) from a
node to the root are called that node's ancestors. Note that
every node is its own ancestor. If a node 
is the ancestor of
node 
, then is called a descendant of . The
tree consisting of all the descendants of of a node n is called its
subtree. The length of the path from a node to the root
is called that node's depth. Thus, the depth of the root
is always 0. In our example, the depth of node 4 is 2.
The preorder list of a tree consists of the root followed by
the preorder list of the subtrees rooted at its children, in order.
For example, the preorder list of tree is 
.
The preorder list of tree 
is (13, 11, 14, 15, 19, 12, 16, 17,
18).
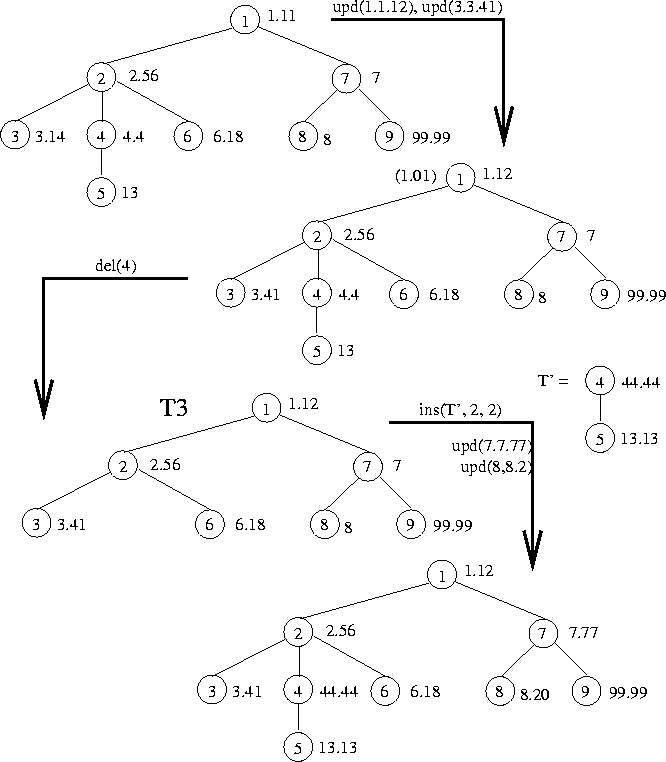
Figure 2: Transforming a tree using an edit script